High-throughput Phenotyping Driven Quantitative Genetics @CMA-FCT-NOVA

class: center, middle, inverse, title-slide

# High-throughput Phenotyping Driven Quantitative Genetics <span class="citation">@CMA-FCT-NOVA</span>
## Decoding mixed model equations
### Gota Morota <br /><a href="http://morotalab.org/">http://morotalab.org/</a> <br />
### 2021/10/20

---

# Acknowledgements
This visit takes place within the scope of the Invited Researcher initiative of the Statistics and Risk Management group of CMA. It  is funded by national funds through the FCT - Fundação para a Ciência e a Tecnologia, I.P., under the scope of the project UIDB/00297/2020 (Center for Mathematics and Applications).

.pull-left[
<img src="NOVA.png" width=200 height=130>
<img src="CMA.png" width=200 height=130>

]

.pull-right[
<img src="NOVAID.png" width=200 height=100>
<img src="FCT.png" width=200 height=120>
<img src="RP.png" width=200 height=130>

]

---
# Single trait linear mixed model 
`$$\mathbf{y = Xb + Zu + e}$$`
<div align="center">
<img src="uni1.png" width=270 height=100>
</div>

- `$\mathbf{X}$`: incidence matrix of systematic effects

- `$\mathbf{Z}$`: incidence matrix of random effects

- `$\mathbf{K}$`: genomic relationship matrix

- `$\mathbf{R}$`: residual relationship matrix

- `$\sigma^2_{u}$`: genomic variance; `$\sigma^2_{e}$`: residual variance

- BLUE: `$\hat{\mathbf{b}} = (\mathbf{X'V^{-1}X})^{-}\mathbf{X'V^{-1}y}$`; BLUP: `$\hat{\mathbf{u}} = \mathbf{KZ'}\mathbf{V^{-1}}(\mathbf{y - X\hat{b}})$`

- where `$\mathbf{V} = \mathbf{ZK\sigma^2_{u}Z' + R\sigma^2_{e}}$`

---
# Mixed model equations (Henderson, 1950)
The corresponding mixed model equations (MME) are
![](uni2.png)

- `$\mathbf{G}^* = \sigma^2_u \mathbf{K}$`

- `$\mathbf{R}^* = \sigma^2_e \mathbf{R}$`

If we multipy `$\mathbf{R}^* = \sigma^2_e\mathbf{I}$` to the both sides
![](uni3.png)

where `$\lambda = \sigma^2_e / \sigma^2_u$`

- MME produces BLUE (E-BLUE) and BLUP (E-BLUP) simultaneously

- [The Origin of BLUP and MME](http://morotalab.org/literature/2015/03/07/The-Origin-of-BLUP-and-MME/)

---
# Decoding single trait MME - Dataset

.pull-left[

| N | Phe  | Env           | Gen  | 
| ------------- |:-------------:| -----:| -----:|
|1| 47      | E1 | G1 |
|2| 51      |  E1     |   G2 |
|3| 46 | E1     |    G3 |
|4| 58 | E1     |    G4 |
|5| 52 | E2     |    G1 |
|6| 46 | E2     |    G2 |
|7| 52 | E2     |    G3 |
|8| 54 | E2     |    G4 |
|9| 53 | E3     |    G1 |
|10| 48 | E3     |    G2 |
|11| 58 | E3     |    G3 |
|12| 52 | E3    |    G4 |
]

.pull-right[
- Phn: Phenotype
- Env: Fixed effect
- Gen: Random effect
]

- Credit: [Alencar Xavier @Corteva](http://alenxav.wixsite.com/home)

---
# What is X?
| N | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|1| 1     | 0 | 0 |
|2| 1      | 0     |   0 |
|3| 1 | 0     |    0 |
|4| 1 | 0     |    0 |
|5| 0 | 1     |    0 |
|6| 0 | 1     |    0 |
|7| 0 | 1     |    0 |
|8| 0 | 1     |    0 |
|9| 0 | 0     |    1 |
|10| 0 | 0     |    1 |
|11| 0 | 0     |    1 |
|12| 0 | 0    |    1 |

- `$\mathbf{X}$` is the 12 x 3 matrix

---
# What is Z?
| N | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|1| 1     | 0 | 0 |0 |
|2| 0      | 1    |   0 |0 |
|3| 0 | 0     |    1 |0 |
|4| 0 | 0     |    0 |1 |
|5| 1 | 0     |    0 |0 |
|6| 0 | 1     |    0 |0 |
|7| 0 | 0     |    1 |0 |
|8| 0 | 0     |    0 |1 |
|9| 1 | 0     |    0 |0 |
|10| 0 | 1     |    0 |0 |
|11| 0 | 0     |    1 |0 |
|12| 0 | 0    |    0 |1 |

- `$\mathbf{Z}$` is the 12 x 4 matrix

---
# What is X'X?

- `$\mathbf{X'}$` is the 3 x 12 matrix

- `$\mathbf{X}$` is the 12 x 3 matrix

- `$\mathbf{X'X}$` is the 3 x 3 matrix

|  | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|EnvE1| 4     | 0 | 0 |
|EnvE2| 0      | 4     |   0 |
|EnvE3| 0 | 0     |    4 |

- `$\mathbf{X'X}$` is the 3 x 3 diagonal matrix counting the number of phenotypes observed in each environment

---
# What is X'Z?

- `$\mathbf{X'}$` is the 3 x 12 matrix

- `$\mathbf{Z}$` is the 12 x 4 matrix

- `$\mathbf{X'Z}$` is the 3 x 4 matrix

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|EnvE1| 1     | 1 | 1 |1 |
|EnvE2| 1      | 1    |   1 |1 |
|EnvE3| 1 | 1     |    1 |1 |

- `$\mathbf{X'Z}$` is the 3 x 4 matrix counting the number of each genotype in each environment

---
# What is Z'X?
- `$\mathbf{Z'}$` is the 4 x 12 matrix

- `$\mathbf{X}$` is the 12 x 3 matrix

- `$\mathbf{X'Z}$` is the 4 x 3 matrix

|  | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|GenG1| 1     | 1 | 1 |
|GenG2| 1      | 1     |   1 |
|GenG3| 1 | 1     |    1 |
|GenG4| 1 | 1     |    1 |

- `$\mathbf{Z'X}$` is the 4 x 3 matrix counting the number of each genotype in each environment

---
# What is Z'Z?
- `$\mathbf{Z'}$` is the 4 x 12 matrix

- `$\mathbf{Z}$` is the 12 x 4 matrix

- `$\mathbf{Z'Z}$` is the 4 x 4 matrix

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|GenG1| 3     | 0 | 0 |0 |
|GenG2| 0      | 3   |   0 |0 |
|GenG3| 0 | 0     |    3 |0 |
|GenG4| 0 |0     |    0 |3|

- `$\mathbf{Z'Z}$` is the 4 x 4 diagonal matrix counting the number of phenotypes observed for each genotype

---
# What is Z'Z + `$\lambda \mathbf{K}^{-1}$`?
- `$\mathbf{Z'}$` is the 4 x 12 matrix

- `$\mathbf{Z}$` is the 12 x 4 matrix

- `$\mathbf{Z'Z}$` is the 4 x 4 matrix

- assume `$\mathbf{K} = \mathbf{I}$` (no relationship)

- `$\lambda = \sigma^2_e / \sigma^2_u = 1.64/9.56 = 0.17$`

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|GenG1| 3.17     | 0 | 0 |0 |
|GenG2| 0      | 3.17   |   0 |0 |
|GenG3| 0 | 0     |    3.17 |0 |
|GenG4| 0 |0     |    0 |3.17|

- `$\mathbf{Z'Z} + \lambda \mathbf{I}$` is the 4 x 4 diagonal matrix counting the number of phenotypes observed for each genotype + `$\lambda$` value in the diagonal elements

---
# What is the left hand side of MME?
<div align="center">
<img src="uni4.png" width=250 height=100>
</div>

|  | EnvE1  | EnvE2           | EnvE3  | GenG1  | GenG2  | GenG3  | GenG4  | 
| ------------- |:-------------:| -----:| -----:|-----:| -----:|-----:| -----:|
|EnvE1| 4     | 0 | 0 |1 |1 |1 |1 |
|EnvE2| 0     | 4 | 0 |1 |1 |1 |1 |
|EnvE3| 0     | 0 | 4 |1 |1 |1 |1 |
|GenG1| 1      | 1     |   1 |3.17 |0 |0 |0 |
|GenG2| 1      | 1     |   1 |0 |3.17 |0 |0 |
|GenG3| 1 | 1     |    1 |0 |0 |3.17 |0 |
|GenG4| 1 | 1     |    1 |0 |0 |0 |3.17 |

---
# What is X'y?
- `$\mathbf{X'}$` is the 3 x 12 matrix

- `$\mathbf{y}$` is the 12 x 1 matrix

- `$\mathbf{X'y}$` is the 3 x 1 matrix

|  |   | 
| ------------- |:-------------:| 
|EnvE1| 202     |
|EnvE2| 204      | 
|EnvE3| 211 |

- `$\mathbf{X'y}$` is the 3 x1 matrix counting the sum of phenotypes in each environment

---
# What is Z'y?
- `$\mathbf{Z'}$` is the 4 x 12 matrix

- `$\mathbf{y}$` is the 12 x 1 matrix

- `$\mathbf{Z'y}$` is the 4 x 1 matrix

|  |   | 
| ------------- |:-------------:| 
|GenG1| 152     |
|GenG2| 145      | 
|GenG3| 156 | 
|GenG4| 164 |

- `$\mathbf{Z'y}$` is the 4 x1 matrix counting the sum of phenotypes for each genotype

---
# What is the right hand side of MME?
<div align="center">
<img src="uni5.png" width=100 height=100>
</div>

|  |   | 
| ------------- |:-------------:| 
|EnvE1| 202     |
|EnvE2| 204      | 
|EnvE3| 211 | 
|GenG1| 152     |
|GenG2| 145      | 
|GenG3| 156 | 
|GenG4| 164 |

---
# Solutions
![](uni6.png)

|  |   | 
| ------------- |:-------------:| 
|EnvE1| 50.50     |
|EnvE2| 51.00      | 
|EnvE3| 52.75 | 
|GenG1| -0.71     |
|GenG2| -2.92      | 
|GenG3| 0.55 | 
|GenG4| 3.08 |

- These are BLUE and BLUP of environments and genotypes, respectively

---
# The role of lambda

BLUE = sum / `$n_{x}$` = the sum of phenotypes in each environment / the number of phenotypes observed in each environment

- BLUE is simply computing averages

BLUP = sum / `$n_{z} + \lambda$` = the sum of phenotypes for each genotype / the number of phenotypes observed for each genotype + `$\lambda$`

- BLUP is shrinked toward zero (proportional to `$\lambda$`)

Note that `$\lambda = \frac{1-h^2}{h^2}$`
- More observations `$\rightarrow$` less shrinkage

- Higher heritability `$\rightarrow$` less shrinkage

---
# Genomic relationship matrix
1: The first type of `$\mathbf{G}$` matrix

`$\mathbf{G} = \frac{\mathbf{W_c}\mathbf{W_c'}}{\sum 2 p_j (1-p_j)}$`

- `$\mathbf{W_c}$`: centered marker matrix

- `$p_j$`: allele frequency at `$j$`th marker

2: The second type of `$\mathbf{G}$` matrix

`$\mathbf{G} = \frac{\mathbf{W_{cs}}\mathbf{W_{cs}'}}{m}$`

- `$\mathbf{W_{cs}}$`: centered and scaled marker matrix

- `$m$`: number of markers

---
# Genomic relationship matrix
![](diagonal.png)

---
# When relationships are known
Suppose `$\mathbf{K}$` is given by

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|GenG1| 1.00     | 0.64 | 0.23 |0.48 |
|GenG2| 0.64      | 1.00   |   0.33 |0.67 |
|GenG3| 0.23 | 0.33     |    1.00 |0.31 |
|GenG4| 0.48 |0.67     |    0.31 |1.00|

Then `$\lambda \mathbf{K}^{-1}$` is

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|GenG1| 0.15     | -0.09 | 0.00 |-0.01 |
|GenG2| -0.09      | 0.22   |   -0.02 |-0.10 |
|GenG3| 0.00 | -0.02     |    0.10 |-0.02 |
|GenG4| -0.01 |-0.10     |    -0.02 |0.17|

- `$\lambda = \sigma^2_e / \sigma^2_u = 1.64/17.70 = 0.09$`

---
# What is the left hand side of MME?
<div align="center">
<img src="uni4.png" width=250 height=100>
</div>

|  | EnvE1  | EnvE2           | EnvE3  | GenG1  | GenG2  | GenG3  | GenG4  | 
| ------------- |:-------------:| -----:| -----:|-----:| -----:|-----:| -----:|
|EnvE1| 4     | 0 | 0 |1 |1 |1 |1 |
|EnvE2| 0     | 4 | 0 |1 |1 |1 |1 |
|EnvE3| 0     | 0 | 4 |1 |1 |1 |1 |
|GenG1| 1      | 1     |   1 |3.15 |-0.09 |0.00 |-0.01 |
|GenG2| 1      | 1     |   1 |-0.09 |3.22 |-0.02 |-0.10 |
|GenG3| 1 | 1     |    1 |0.00 |-0.02 |3.10 |-0.02 |
|GenG4| 1 | 1     |    1 |-0.01 |-0.10 |-0.02 |3.17 |

---
# When there are missing phenotypes
.pull-left[
| N | Phe  | Env           | Gen  | 
| ------------- |:-------------:| -----:| -----:|
|1| 47      | E1 | G1 |
|2| 51      |  E1     |   G2 |
|3| NA | E1     |    G3 |
|4| 58 | E1     |    G4 |
|5| 52 | E2     |    G1 |
|6| 46 | E2     |    G2 |
|7| 52 | E2     |    G3 |
|8| NA | E2     |    G4 |
|9| 53 | E3     |    G1 |
|10| 48 | E3     |    G2 |
|11| 58 | E3     |    G3 |
|12| 52 | E3    |    G4 |
]

.pull-right[
<iframe src="https://giphy.com/embed/3o85xpBDDNSAQsbu2A" width="480" height="360" frameBorder="0" class="giphy-embed" allowFullScreen></iframe><p><a href="https://giphy.com/gifs/afvbabies-babies-afv-3o85xpBDDNSAQsbu2A">via GIPHY</a></p>
]

---
# What is X?

| N | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|1| 1     | 0 | 0 |
|2| 1      | 0     |   0 |
|4| 1 | 0     |    0 |
|5| 0 | 1     |    0 |
|6| 0 | 1     |    0 |
|7| 0 | 1     |    0 |
|9| 0 | 0     |    1 |
|10| 0 | 0     |    1 |
|11| 0 | 0     |    1 |
|12| 0 | 0    |    1 |

- Remove missing rows

- `$\mathbf{X}$` is the 10 x 3 matrix

---
# What is Z?

| N | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|1| 1     | 0 | 0 |0 |
|2| 0      | 1    |   0 |0 |
|4| 0 | 0     |    0 |1 |
|5| 1 | 0     |    0 |0 |
|6| 0 | 1     |    0 |0 |
|7| 0 | 0     |    1 |0 |
|9| 1 | 0     |    0 |0 |
|10| 0 | 1     |    0 |0 |
|11| 0 | 0     |    1 |0 |
|12| 0 | 0    |    0 |1 |

- Remove missing rows

- `$\mathbf{Z}$` is the 10 x 4 matrix

---
# What is X'X?

- `$\mathbf{X'}$` is the 3 x 10 matrix

- `$\mathbf{X}$` is the 10 x 3 matrix

- `$\mathbf{X'X}$` is the 3 x 3 matrix

|  | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|EnvE1| 3     | 0 | 0 |
|EnvE2| 0      | 3     |   0 |
|EnvE3| 0 | 0     |    4 |

- `$\mathbf{X'X}$` is the 3 x 3 diagonal matrix counting the number of phenotypes observed in each environment

---
# What is X'Z?

- `$\mathbf{X'}$` is the 3 x 10 matrix

- `$\mathbf{Z}$` is the 10 x 4 matrix

- `$\mathbf{X'Z}$` is the 3 x 4 matrix

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|EnvE1| 1     | 1 | 0 |1 |
|EnvE2| 1      | 1    |   1 |0 |
|EnvE3| 1 | 1     |    1 |1 |

- `$\mathbf{X'Z}$` is the 3 x 4 matrix counting the number of each genotype in each environment

---
# What is Z'X?
- `$\mathbf{Z'}$` is the 4 x 10 matrix

- `$\mathbf{X}$` is the 10 x 3 matrix

- `$\mathbf{X'Z}$` is the 4 x 3 matrix

|  | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|GenG1| 1     | 1 | 1 |
|GenG2| 1      | 1     |   1 |
|GenG3| 0 | 1     |    1 |
|GenG4| 1 | 0     |    1 |

- `$\mathbf{Z'X}$` is the 4 x 3 matrix counting the number of each genotype in each environment

---
# What is Z'Z?
- `$\mathbf{Z'}$` is the 4 x 10 matrix

- `$\mathbf{Z}$` is the 4 x 10 matrix

- `$\mathbf{Z'Z}$` is the 4 x 4 matrix

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|GenG1| 3     | 0 | 0 |0 |
|GenG2| 0      | 3   |   0 |0 |
|GenG3| 0 | 0     |    2 |0 |
|GenG4| 0 |0     |    0 |2|

- `$\mathbf{Z'Z}$` is the 4 x 4 diagonal matrix counting the number of phenotypes observed for each genotype

---
# What is the left hand side of MME?
<div align="center">
<img src="uni4.png" width=250 height=100>
</div>

|  | EnvE1  | EnvE2           | EnvE3  | GenG1  | GenG2  | GenG3  | GenG4  | 
| ------------- |:-------------:| -----:| -----:|-----:| -----:|-----:| -----:|
|EnvE1| 3     | 0 | 0 |1 |1 |0 |1 |
|EnvE2| 0     | 3 | 0 |1 |1 |1 |0 |
|EnvE3| 0     | 0 | 4 |1 |1 |1 |1 |
|GenG1| 1      | 1     |   1 |3.10 |-0.06 |0.00 |-0.01 |
|GenG2| 1      | 1     |   1 |-0.06 |3.15 |-0.01 |-0.07 |
|GenG3| 0 | 1     |    1 |0.00 |-0.01 |2.07 |-0.01 |
|GenG4| 1 | 0     |    1 |-0.01 |-0.07 |-0.01 |2.11 |

- `$\lambda = \sigma^2_e / \sigma^2_u = 1.64/19.61 = 0.06$`

---
# What is the right hand side of MME?
<div align="center">
<img src="uni5.png" width=100 height=100>
</div>

|  |   | 
| ------------- |:-------------:| 
|EnvE1| 156     |
|EnvE2| 150      | 
|EnvE3| 211 | 
|GenG1| 152     |
|GenG2| 145      | 
|GenG3| 110 | 
|GenG4| 110 |

---
# Today's lunch 
.pull-left[
<img src="arrozdepolvo.jpg" width=350 height=350>
Arroz de Polvo 
]

.pull-rigth[
<img src="pudding.jpg" width=350 height=350>
Pudim de Ovos
]

---
# The first genotype is missing phenotypes
.pull-left[
| N | Phe  | Env           | Gen  | 
| ------------- |:-------------:| -----:| -----:|
|1| NA      | E1 | G1 |
|2| 51      |  E1     |   G2 |
|3| 46 | E1     |    G3 |
|4| 58 | E1     |    G4 |
|5| NA | E2     |    G1 |
|6| 46 | E2     |    G2 |
|7| 52 | E2     |    G3 |
|8| 54 | E2     |    G4 |
|9| NA | E3     |    G1 |
|10| 48 | E3     |    G2 |
|11| 58 | E3     |    G3 |
|12| 52 | E3    |    G4 |
]

.pull-right[
<center>
<iframe src="https://giphy.com/embed/lKZEeXJGhU1d6" width="300" height="350" frameBorder="0" class="giphy-embed" allowFullScreen></iframe><p><a href="https://giphy.com/gifs/scared-despicable-me-lKZEeXJGhU1d6">via GIPHY</a>
</p>
</center>
]

---
# What is X?
| N | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|2| 1      | 0     |   0 |
|3| 1 | 0     |    0 |
|4| 1 | 0     |    0 |
|6| 0 | 1     |    0 |
|7| 0 | 1     |    0 |
|8| 0 | 1     |    0 |
|10| 0 | 0     |    1 |
|11| 0 | 0     |    1 |
|12| 0 | 0    |    1 |

- Remove missing rows

- `$\mathbf{X}$` is the 9 x 3 matrix

---
# What is Z?
| N | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|2| 0      | 1    |   0 |0 |
|3| 0 | 0     |    1 |0 |
|4| 0 | 0     |    0 |1 |
|6| 0 | 1     |    0 |0 |
|7| 0 | 0     |    1 |0 |
|8| 0 | 0     |    0 |1 |
|10| 0 | 1     |    0 |0 |
|11| 0 | 0     |    1 |0 |
|12| 0 | 0    |    0 |1 |

- Remove missing rows

- `$\mathbf{Z}$` is the 9 x 4 matrix

---
# What is X'X?

- `$\mathbf{X'}$` is the 3 x 9 matrix

- `$\mathbf{X}$` is the 9 x 3 matrix

- `$\mathbf{X'X}$` is the 3 x 3 matrix

|  | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|EnvE1| 3     | 0 | 0 |
|EnvE2| 0      | 3     |   0 |
|EnvE3| 0 | 0     |    3 |

- `$\mathbf{X'X}$` is the 3 x 3 diagonal matrix counting the number of phenotypes observed in each environment

---
# What is X'Z?

- `$\mathbf{X'}$` is the 3 x 9 matrix

- `$\mathbf{Z}$` is the 9 x 4 matrix

- `$\mathbf{X'Z}$` is the 3 x 4 matrix

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|EnvE1| 0     | 1 | 1 |1 |
|EnvE2| 0      | 1    |   1 |1 |
|EnvE3| 0 | 1     |    1 |1 |

- `$\mathbf{X'Z}$` is the 3 x 4 matrix counting the number of each genotype in each environment

---
# What is Z'X?
- `$\mathbf{Z'}$` is the 4 x 12 matrix

- `$\mathbf{X}$` is the 12 x 3 matrix

- `$\mathbf{X'Z}$` is the 4 x 3 matrix

|  | EnvE1  | EnvE2           | EnvE3  | 
| ------------- |:-------------:| -----:| -----:|
|GenG1| 0     | 0 | 0 |
|GenG2| 1      | 1     |   1 |
|GenG3| 1 | 1     |    1 |
|GenG4| 1 | 1     |    1 |

- `$\mathbf{Z'X}$` is the 4 x 3 matrix counting the number of each genotype in each environment

---
# What is Z'Z?
- `$\mathbf{Z'}$` is the 4 x 9 matrix

- `$\mathbf{Z}$` is the 4 x 9 matrix

- `$\mathbf{Z'Z}$` is the 4 x 4 matrix

|  | GenG1  | GenG2           | GenG3  | GenG4 | 
| ------------- |:-------------:| -----:| -----:| -----:|
|GenG1| 0     | 0 | 0 |0 |
|GenG2| 0      | 3   |   0 |0 |
|GenG3| 0 | 0     |    3 |0 |
|GenG4| 0 |0     |    0 |3|

- `$\mathbf{Z'Z}$` is the 4 x 4 diagonal matrix counting the number of phenotypes observed for each genotype

---
# What is the left hand side of MME?
<div align="center">
<img src="uni4.png" width=250 height=100>
</div>

|  | EnvE1  | EnvE2           | EnvE3  | GenG1  | GenG2  | GenG3  | GenG4  | 
| ------------- |:-------------:| -----:| -----:|-----:| -----:|-----:| -----:|
|EnvE1| 3     | 0 | 0 |0 |1 |0 |1 |
|EnvE2| 0     | 3 | 0 |0 |1 |1 |0 |
|EnvE3| 0     | 0 | 3 |0 |1 |1 |1 |
|GenG1| 0      | 0     |   0 |0.14 |-0.08 |0.00 |-0.01 |
|GenG2| 1      | 1     |   1 |-0.08 |3.19 |-0.02 |-0.09 |
|GenG3| 0 | 1     |    1 |0.00 |-0.02 |3.09 |-0.01 |
|GenG4| 1 | 0     |    1 |-0.01 |-0.09 |-0.01 |3.15 |

- `$\lambda = \sigma^2_e / \sigma^2_u = 1.79/22.78 = 0.08$`

---
# What is the right hand side of MME?
<div align="center">
<img src="uni5.png" width=100 height=100>
</div>

|  |   | 
| ------------- |:-------------:| 
|EnvE1| 155    |
|EnvE2| 152      | 
|EnvE3| 158 | 
|GenG1| 0     |
|GenG2| 145      | 
|GenG3| 156 | 
|GenG4| 164 |

---
# Solutions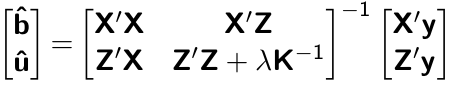
![](uni6.png)

|  |   | 
| ------------- |:-------------:| 
|EnvE1| 52.06     |
|EnvE2| 51.06      | 
|EnvE3| 53.06 | 
|GenG1| -1.82     |
|GenG2| -3.48      | 
|GenG3| -0.07 | 
|GenG4| 2.38 |

- These are BLUE and BLUP of environments and genotypes, respectively

---
# Dimension of left hand side
<div align="center">
<img src="equDecoded.png" width=300 height=250>
</div>

.pull-left[
- s: number of unique fixed effects

- q: number of unique genotypes

- does not depend on `$n$`
]

.pull-right[
<center>
<iframe src="https://giphy.com/embed/UgD64OxiNyTBK" width="421" height="250" frameBorder="0" class="giphy-embed" allowFullScreen></iframe><p><a href="https://giphy.com/gifs/funny-lol-guitarhero-UgD64OxiNyTBK">via GIPHY</a></p>
</center>
]

---
# Extending a linear mixed model for GWAS
Previous model 
`$$\mathbf{y = Xb + Zu + e}$$`
</br>

Linear mixed model single-marker regression 
`$$\mathbf{y = Xb + Wa + Zu + e}$$`

- `$\mathbf{W}$`: marker matrix

- `$\mathbf{a}$`: vector of marker effect

---
# Linear mixed model for GWAS 
Single marker-based mixed model association (MMA)
`\begin{align*}
\mathbf{y} &= \mu + \mathbf{w_ja_j} + \mathbf{Zg} + \boldsymbol{\epsilon} \\
\mathbf{g} &\sim N(0, \mathbf{G}\sigma^2_{g})
\end{align*}`

`$\mathbf{G}$` captures population structure and polygenic effects

Double counting?

Alternatively, 
`\begin{align*}
\mathbf{y} &= \mu + \mathbf{w_ja_j} + \mathbf{Zg} + \boldsymbol{\epsilon} \\
\mathbf{g} &\sim N(0, \mathbf{G}_{-k}\sigma^2_{g_{-k}})
\end{align*}`
where `$-k$` denotes the `$k$`th chromosome removed

See
* Rincent et al. 2014. ([10.1534/genetics.113.159731](https://doi.org/10.1534/genetics.113.159731))

* Chen and Lipka. 2016. ([10.1534/g3.116.029090](https://doi.org/10.1534/g3.116.029090))

---
# How to solve the linear mixed model?

1:  Mixed model equations (MME)
`\begin{align*}
\mathbf{y} &= \mu + \mathbf{w_ja_j} + \mathbf{Zg} + \boldsymbol{\epsilon} \\
\end{align*}`

The mixed model equations of [Henderson (1949)](http://morotalab.org/literature/pdf/henderson1949.pdf) are given by

2:  Weighted least squares
`\begin{align*}
  \hat{\mathbf{a}} &= (\mathbf{W'U T U'W})^{-1}\mathbf{W'U} \mathbf{T} \mathbf{U'y} 
\end{align*}`
where

- `$\mathbf{U}$`: eigenvectors of the `$\mathbf{G}$` matrix
- `$\mathbf{D}$`: eigenvalues of the `$\mathbf{G}$` matrix

`\begin{align*}
\mathbf{T} = [\mathbf{D}  + \lambda \mathbf{I}  ]^{-1}
\end{align*}`

---
# Important literature
Animal

* [Kennedy et al. 1992.](https://doi.org/10.2527/1992.7072000x) Estimation of effects of single genes on quantitative traits. J Anim Sci. 70:2000-2012.

Plant

* [Yu et al. 2006.](https://dx.doi.org/10.1038/ng1702) A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet. 38:203-208.

---
# Bibliography
![](biblio.png)