class: center, middle, inverse, title-slide # Structural equation model GWAS ## Quantitative Genetics Short Course <span class="citation">@UFV</span> ### Gota Morota <br /><a href="http://morotalab.org/" class="uri">http://morotalab.org/</a> <br /> ### 2019/11/25 --- # Multivariate traits  - Multi-trait GWAS (MTM-GWAS) - Structural equation model GWAS (SEM-GWAS) --- # Multi-trait model $$ `\begin{align*} \mathbf{y} &= \mathbf{Xb} + \mathbf{Zu} + \mathbf{e} \\ \begin{bmatrix} \mathbf{y_1} \\ \mathbf{y_2} \\ \vdots \\ \mathbf{y_n} \\ \end{bmatrix} &= \begin{bmatrix} \mathbf{X_1} & 0 & \cdots & 0 \\ 0 & \mathbf{X_2} & \cdots & 0\\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \mathbf{X_n} \\ \end{bmatrix} \begin{bmatrix} \mathbf{b_1} \\ \mathbf{b_2} \\ \vdots \\ \mathbf{b_n} \end{bmatrix} \\ &+ \begin{bmatrix} \mathbf{Z_1} & 0 & \cdots & 0 \\ 0 & \mathbf{Z_2} & \cdots & 0\\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \mathbf{Z_n} \\ \end{bmatrix} \begin{bmatrix} \mathbf{u_1} \\ \mathbf{u_2} \\ \vdots \\ \mathbf{u_n} \end{bmatrix} + \begin{bmatrix} \mathbf{e_1} \\ \mathbf{e_2} \\ \vdots \\ \mathbf{e_n} \end{bmatrix} \\ E\begin{pmatrix} \mathbf{u} \\ \mathbf{e} \end{pmatrix} &= \begin{bmatrix} 0 \\ 0 \end{bmatrix} \\ Var\begin{pmatrix} \mathbf{u} \\ \mathbf{e} \end{pmatrix} &= \begin{bmatrix} \mathbf{\Sigma^2_{g}} \otimes \mathbf{G} & 0 \\ 0 & \mathbf{\Sigma^2_e} \otimes \mathbf{I} \end{bmatrix} \end{align*}` $$ --- # Multi-trait model (t = 2) $$ `\begin{align*} \mathbf{\Sigma^2_{g}} &= \begin{bmatrix} \mathbf{\Sigma^2_{g_{1}}} & \mathbf{\Sigma^2_{g_{12}}} \\ \mathbf{\Sigma^2_{g_{21}}} & \mathbf{\Sigma^2_{g_{2}}} \end{bmatrix} \\ \mathbf{\Sigma^2_{e}} &= \begin{bmatrix} \mathbf{\Sigma^2_{e_{1}}} & \mathbf{\Sigma^2_{e_{12}}} \\ \mathbf{\Sigma^2_{e_{21}}} & \mathbf{\Sigma^2_{e_{2}}} \end{bmatrix} \\ \mathbf{\Sigma^2_{g}} \otimes \mathbf{G} &= \begin{bmatrix} \mathbf{\Sigma^2_{g_{1}}} \mathbf{G} & \mathbf{\Sigma^2_{g_{12}}} \mathbf{G} \\ \mathbf{\Sigma^2_{g_{21}}} \mathbf{G} & \mathbf{\Sigma^2_{g_{2}}} \mathbf{G} \end{bmatrix} \\ \mathbf{\Sigma^2_{e}} \otimes \mathbf{I} &= \begin{bmatrix} \mathbf{\Sigma^2_{e_{1}}} \mathbf{I} & \mathbf{\Sigma^2_{e_{12}}} \mathbf{I} \\ \mathbf{\Sigma^2_{e_{21}}} \mathbf{I} & \mathbf{\Sigma^2_{e_{2}}} \mathbf{I} \end{bmatrix} \\ \end{align*}` $$ --- # Multi-trait model (t = 2) The MME model is $$ `\begin{align*} \begin{bmatrix} \mathbf{X'R_0^{-1}X} & \mathbf{X'R_0^{-1}Z} \\ \mathbf{Z'R_0^{-1}X} & \mathbf{Z'R_0^{-1}Z} + \mathbf{G_0}^{-1} \\ \end{bmatrix} \begin{bmatrix} \mathbf{b} \\ \mathbf{u} \end{bmatrix} &= \begin{bmatrix} \mathbf{X'R_0^{-1}y} \\ \mathbf{Z'R_0^{-1}y} \end{bmatrix} \\ \mathbf{G_0}^{-1} &= (\mathbf{\Sigma^2_{g}} \otimes \mathbf{G})^{-1} \\ &= \mathbf{\Sigma^2_{g}}^{-1} \otimes \mathbf{G}^{-1} \\ \mathbf{R_0}^{-1} &= (\mathbf{\Sigma^2_{e}} \otimes \mathbf{I})^{-1} \\ &= {\mathbf{\Sigma^2_{e}}}^{-1} \otimes \mathbf{I}^{-1} \end{align*}` $$ --- # Multi-trait GBLUP model `$$\mathbf{y_{1} = X_{1}b_{1} + Z_{1}u_{1} + e_{1}}$$` `$$\mathbf{y_{2} = X_{2}b_{2} + Z_{2}u_{2} + e_{2}}$$` Individuals within traits 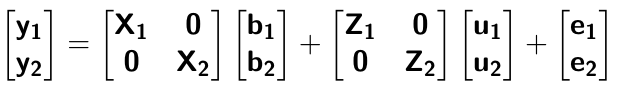 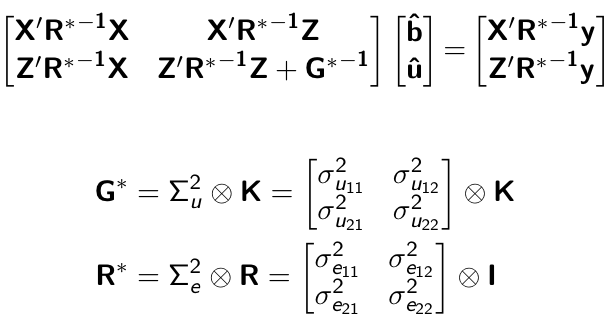 --- # Multi-trait RR-BLUP model `$$\mathbf{y_{1} = X_{1}b_{1} + W_{1}a_{1} + e_{1}}$$` `$$\mathbf{y_{2} = X_{2}b_{2} + W_{2}a_{2} + e_{2}}$$` Individuals within traits 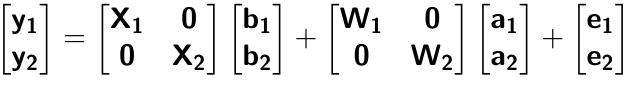 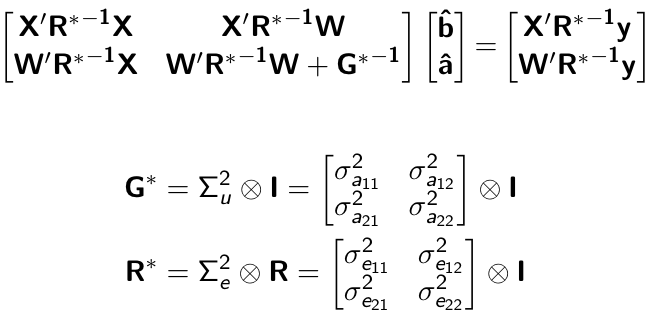 --- # Is multi-trait model useful? GBLUP model - estimate covariance structures `\(\rightarrow\)` genetic correlations - traits with scarce records - traits with low heritability RR-BLUP - increase statistical power to detect QTL regions --- # MTM-GWAS <img src="MTMGWAS.png" height="406px" width="650px"/> --- # Multiple-trait GWAS (MTM-GWAS) <img src="MTM.png" height="506px" width="750px"/> --- # Interrelationships among traits 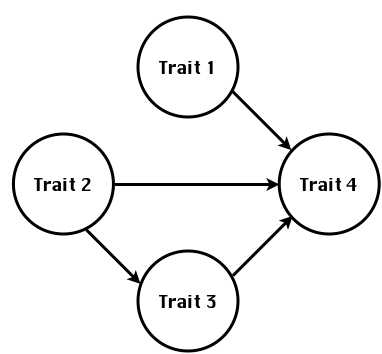 1. Biological prior - previous experiments - literature 2. Infer from the data --- # Phenotypic, genetic, and residual networks 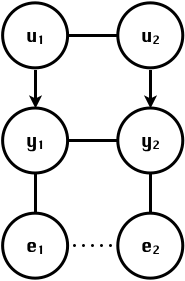 --- # Leveraging phenotypic networks to study multiple traits  --- # Leveraging phenotypic networks to study multiple traits  --- # Introducing SEM into the GWAS framework 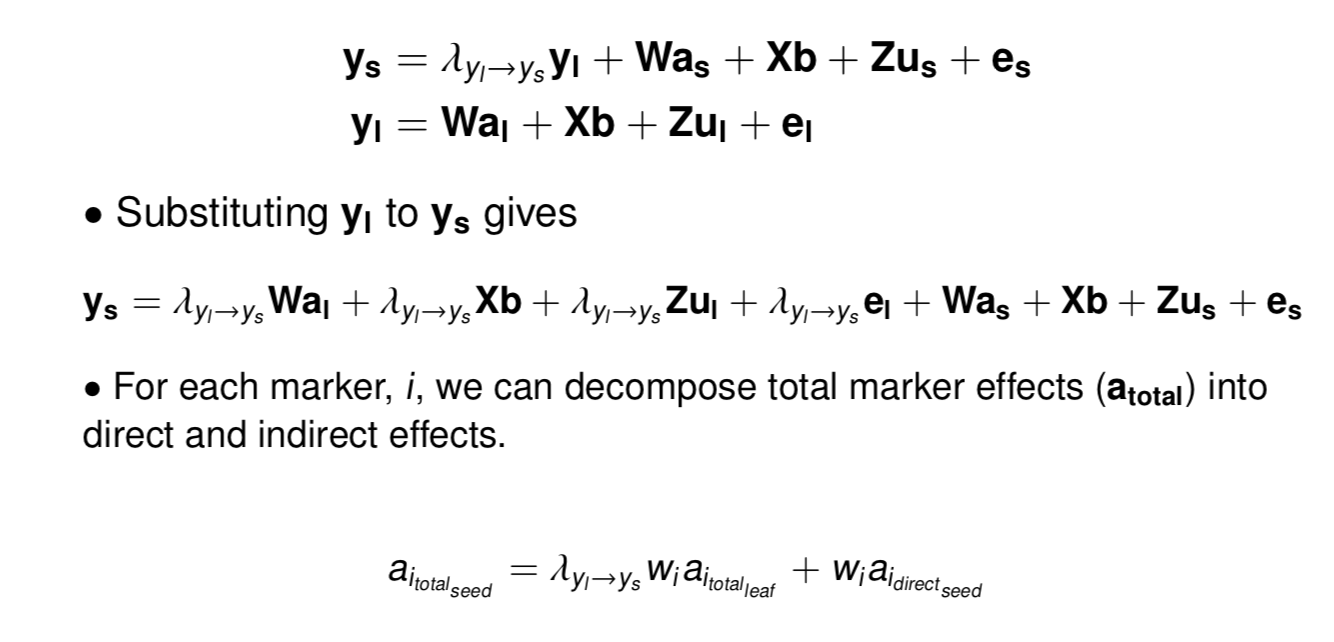 --- # Structural equation model GWAS (SEM-GWAS) Direct effect of SNP on Trait 4 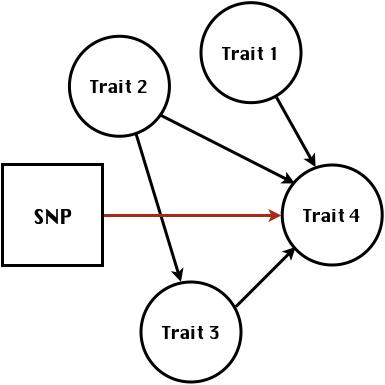 --- # SEM-GWAS Indirect effect of SNP on Trait 4 through Trait 1 (1) 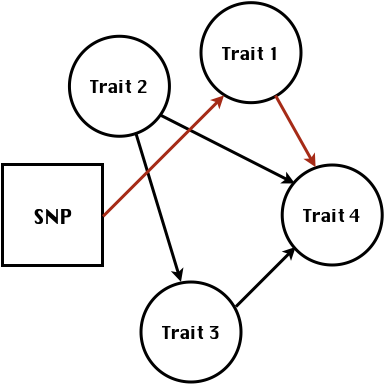 --- # SEM-GWAS Indirect effect of SNP on Trait 4 through Trait 2 (2) 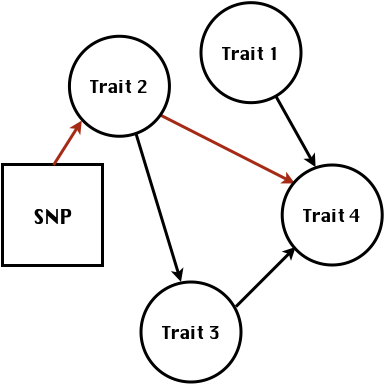 --- # SEM-GWAS Indirect effect of SNP on Trait 4 through Trait 2 & 3 (3) 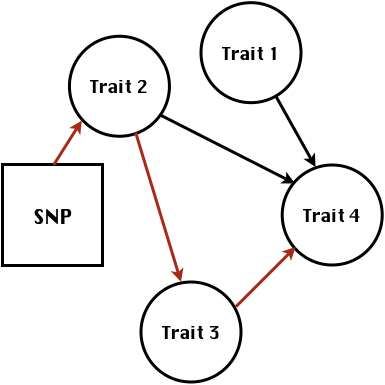 --- # SEM-GWAS Indirect effect of SNP on Trait 4 through Trait 3 (4)  --- # SEM-GWAS vs. MTM-GWAS Effect of SNP on Trait 4 <img src="MTM4.png" height="306px" width="400px"/> `\begin{align*} \text{Effect of SNP (MTM-GWAS)} &\approx \text{Overall effect (SEM-GWAS)}\\ &= \text{Direct effect (SEM-GWAS)} \\ &+ \text{Indirect effect (SEM-GWAS)} \end{align*}` --- # How to fit SEM-GWAS? 1. Fit MTM and decompose phenotypes into genetics and residuals 2. Infer the network structure of traits 3. Fit SEM-GWAS given the network structure Example 1: Chicken data (n = 1,351), Momen et al. (2018) - breast muscle (BM) - body weight (BW) - hen-house egg production (HHP) --- # Inferred network structure (1) <img src="chickenSEM1.png" height="276px" width="600px"/> Structual equation model <img src="chickenSEM5.png" height="166px" width="500px"/> --- # Inferred network structure (2) <img src="chickenSEM1.png" height="276px" width="600px"/> Structual equation model <img src="chickenSEM3.png" height="56px" width="250px"/> <img src="chickenSEM4.png" height="106px" width="500px"/> --- # Inferred network structure (3) <img src="chickenSEM1.png" height="276px" width="600px"/> Decomposition of SNP effects <img src="chickenSEM2.png" height="176px" width="500px"/> --- # Manhattan plots of BW (overall, direct, and indirect SNP effects) <img src="chickenSEM6.png" height="426px" width="560px"/> --- # More details about Chicken SEM-GWAS <img src="frontiers.png" height="400px" width="630px"/> --- # Leveraging phenotypic networks to study multiple traits  --- # Leveraging phenotypic networks to study multiple traits  .pull-left[ - Shoot biomass (projected shoot area, PSA) - Root biomass (RB) ] .pull-right[ - Water use (WU) - Water use efficiency (WUE) ] How are these traits related? --- # Rice data - Drought data - Rice diversity panel - Projected shoot area - Root biomass - Water use efficiency - Water use Inferred trait network structure <img src="riceSEM1.png" height="326px" width="460px"/> --- # Bayesian networks .pull-left[  ] .pull-right[ - BN based on 500 bootstrap samples - % above edges indicate percentage of bootstrap networks with the given edge - Numbers in parenthesis indicate the proportion of bootstrap networks with the given edge direction ] --- # Bayesian networks .pull-left[  ] .pull-right[ - Phenotypic values for WUE are dependant on phenotypes for RB and PSA - Phenotypic values for WU are dependant on phenotypes for PSA ] --- # How to fit SEM-GWAS? `\begin{align*} \mathbf{y} =\boldsymbol{\Lambda} \mathbf{y} + \mathbf{ws} + \mathbf{Zg} + \boldsymbol{\epsilon} \end{align*}` <img src="riceSEM2.png" height="426px" width="600px"/> --- # Inferred trait network structure <img src="riceSEM3.png" height="426px" width="700px"/> --- # Structural equation model <img src="riceSEM4.png" height="426px" width="700px"/> --- # Bayesian information criterion <img src="riceSEM10.png" height="306px" width="620px"/> --- # Structural coefficients <img src="riceSEM11.png" height="306px" width="610px"/> --- # Projected shoot area `\begin{align*} \text{Direct}_{s_j \rightarrow y_{1_{\text{PSA}}}} &= s_{j(y_{1_{\text{PSA}}})} \\ \text{Total}_{s_j \rightarrow y_{1_{\text{PSA}}}} &= \text{Direct}_{s_j \rightarrow y_{1_{\text{PSA}}}}\\ &= s_{j(y_{1_{\text{PSA}}})} \end{align*}` <img src="riceSEM5.png" height="406px" width="700px"/> --- # Root biomass `\begin{align*} \text{Direct}_{s_j \rightarrow y_{2_{\text{RB}}}} &=s_{j(y_{2_{\text{RB}}})} \\ \text{Total}_{s_j \rightarrow y_{2_{\text{RB}}}} &= \text{Direct}_{s_j \rightarrow y_{2_{\text{RB}}}}\\ &= s_{j(y_{2_{\text{RB}}})} \end{align*}` <img src="riceSEM5.png" height="406px" width="700px"/> --- # Water use `\begin{align*} \text{Direct}_{s_j \rightarrow y_{3_{\text{WU}}}} &=s_{j(y_{3_{\text{WU}}})} \\ \text{Indirect}_{s_j \rightarrow y_{3_{\text{WU}}}} &= \lambda_{13}s_{j(y_{1_{\text{PSA}}})} \\ \text{Total}_{s_j \rightarrow y_{3_{\text{WU}}}} &= \text{Direct}_{s_j \rightarrow y_{3_{\text{WU}}}} + \text{Indirect}_{s_j \rightarrow y_{3_{\text{WU}}}} \\ &= s_{j(y_{3_{\text{WU}}})} + \lambda_{13}s_{j(y_{1_{\text{PSA}}})} \end{align*}` <img src="riceSEM7.png" height="336px" width="700px"/> --- # Water use efficiency `\begin{align*} \text{Direct}_{s_j \rightarrow y_{4_{\text{WUE}}}} &=s_{j(y_{4_{\text{WUE}}})} \\ \text{Indirect(1)}_{s_j \rightarrow y_{4_{\text{WUE}}}} &= \lambda_{14}s_{j(y_{1_{\text{PSA}}})} \\ \text{Indirect(2)}_{s_j \rightarrow y_{4_{\text{WUE}}}} &= \lambda_{24}s_{j(y_{2_{\text{RB}}})} \\ \text{Total}_{S_j \rightarrow y_{4_{\text{WUE}}}} &= \text{Direct}_{s_j \rightarrow y_{4_{\text{WUE}}}} + \text{Indirect(1)}_{s_j \rightarrow y_{4_{\text{WUE}}}} + \text{Indirect(2)}_{s_j \rightarrow y_{4_{\text{WUE}}}} \\ &= s_{j(y_{4_{\text{WUE}}})} + \lambda_{14}s_{j(y_{1_{\text{PSA}}})} + \lambda_{24}s_{j(y_{2_{\text{RB}}})} \end{align*}` --- # Water use efficiency <img src="riceSEM8.png" height="536px" width="700px"/> --- # Ongoing SEM-GWAS projects - Italian Brown Swiss cattle (University of Padua) - Milk yield - Milk pH - Milk lactose - Somatic cell score - Non-casein N --- # Conclusions for SEM-GWAS - Relatively simple approach to understand how QTL affect multiple traits - Provides novel insights compared to conventional multi-trait GWAS approaches