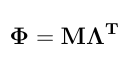Random Regression

List

Standardize time points covariate

R script: stdtime.txt
Literature: Mrode, R.A. 2005. Linear Models for the Prediction of Animal Breeding Values. CAB International, Oxon, UK.

Given time points covariate and order of fit for Legendre polynomials, return matrix 'M' containing the polynomials of standardized time. 'M' is order t (number of time points) by k (order of Legendre polynomials). Here is an example from Mrode (2005), fitting the Legendre polynomials of order 4 on DIM (Days In Milk).

> DIM <- c(4,38,72,106,140,174,208,242,276,310)
> order <- 4
> stdtime(DIM, order)
      [,1]       [,2]       [,3]         [,4]         [,5]
 [1,]    1 -1.0000000 1.00000000 -1.000000000 1.0000000000
 [2,]    1 -0.7777778 0.60493827 -0.470507545 0.3659503125
 [3,]    1 -0.5555556 0.30864198 -0.171467764 0.0952598689
 [4,]    1 -0.3333333 0.11111111 -0.037037037 0.0123456790
 [5,]    1 -0.1111111 0.01234568 -0.001371742 0.0001524158
 [6,]    1  0.1111111 0.01234568  0.001371742 0.0001524158
 [7,]    1  0.3333333 0.11111111  0.037037037 0.0123456790
 [8,]    1  0.5555556 0.30864198  0.171467764 0.0952598689
 [9,]    1  0.7777778 0.60493827  0.470507545 0.3659503125
[10,]    1  1.0000000 1.00000000  1.000000000 1.0000000000

Legendre Polynomials

R script: legendre.txt
Literature 1: Mrode, R.A. 2005. Linear Models for the Prediction of Animal Breeding Values. CAB International, Oxon, UK.
Literature 2: Gengler, N. et. al. 1999. Estimation of (Co)variance Function Coefficients for Test Day Yield with a Expectation-Maximization Restricted Maximum Likelihood Algorithm. Journal of Dairy Science. 82

Return coefficient matrix (lambda) of n-th order Legendre polynomials. Scaling method implemented by Gengler et. al. (1999) converts constant Legendre polynomial coefficients into 1.

> legendre(4, gengler=FALSE)
           [,1]      [,2]      [,3]     [,4]     [,5]
[1,]  0.7071068  0.000000  0.000000 0.000000 0.000000
[2,]  0.0000000  1.224745  0.000000 0.000000 0.000000
[3,] -0.7905694  0.000000  2.371708 0.000000 0.000000
[4,]  0.0000000 -2.806243  0.000000 4.677072 0.000000
[5,]  0.7954951  0.000000 -7.954951 0.000000 9.280777

> legendre(4, gengler=TRUE)
          [,1]      [,2]       [,3]     [,4]   [,5]
[1,]  1.000000  0.000000   0.000000 0.000000  0.000
[2,]  0.000000  1.732051   0.000000 0.000000  0.000
[3,] -1.118034  0.000000   3.354102 0.000000  0.000
[4,]  0.000000 -3.968627   0.000000 6.614378  0.000
[5,]  1.125000  0.000000 -11.250000 0.000000 13.125

The first row is the constant coefficient. The second row is the 1st order polynomial. The third row is the 2nd order polynomial, and so on.

Now we can get a matrix of Legendre polynomials evaluated at the different DIM. This matrix is given by following equation.

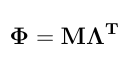
> DIM <- c(4,38,72,106,140,174,208,242,276,310)
> order <- 4
> M <- stdtime(DIM, order)
> Lambda <- legendre(order, gengler=FALSE)
> Phi <- M%*%t(Lambda)
> Phi
           [,1]       [,2]       [,3]        [,4]        [,5]
 [1,] 0.7071068 -1.2247449  1.5811388 -1.87082869  2.12132034
 [2,] 0.7071068 -0.9525793  0.6441677 -0.01796406 -0.62045629
 [3,] 0.7071068 -0.6804138 -0.0585607  0.75705688 -0.77565120
 [4,] 0.7071068 -0.4082483 -0.5270463  0.76218947  0.02618914
 [5,] 0.7071068 -0.1360828 -0.7612891  0.30538905  0.69870039
 [6,] 0.7071068  0.1360828 -0.7612891 -0.30538905  0.69870039
 [7,] 0.7071068  0.4082483 -0.5270463 -0.76218947  0.02618914
 [8,] 0.7071068  0.6804138 -0.0585607 -0.75705688 -0.77565120
 [9,] 0.7071068  0.9525793  0.6441677  0.01796406 -0.62045629
[10,] 0.7071068  1.2247449  1.5811388  1.87082869  2.12132034